Pokémon Picross - Pique-rosse ? Pakomprilol... Introduction aux picross
Picross, c’est quoi ?
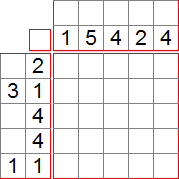
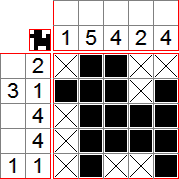
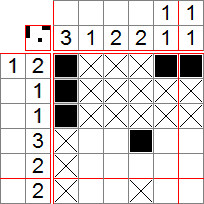
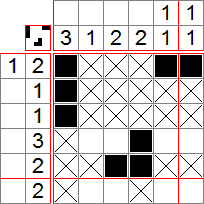
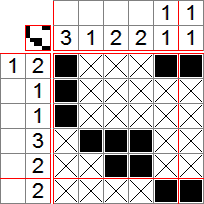
Le picross, ou encore logigraphe, griddler, nonogram, est un jeu de logique qui consiste à colorier des cases pour découvrir un dessin en prenant en compte des indices. On peut faire des picross de toutes les tailles et formes et il existe beaucoup de variantes. Voici par exemple un Picross 5x5 :
Dans Pokémon Picross, les grilles de jeu font 10x10, 15x15 ou 20x15 cases, sauf les toutes premières grilles du jeu, qui sont des 5x5.
Ok, mais comment on résout ce truc ?
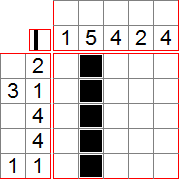
Reprenons l’exemple ci-dessus. Les chiffres-indices indiquent le nombre de cases à remplir sur chaque ligne/colonne. Par exemple, le 2 à côté de la première ligne indique qu’il y a 2 cases consécutives à noircir sur la ligne. Similairement, le (3 1) à côté de la deuxième ligne signifie qu’il y a 3 cases noires consécutives, suivies d’un certain nombre de cases vides, puis 1 case noire isolée. Pour bien commencer une grille, il faut repérer les grands nombres. Ici, nous avons un 5 sur une colonne, ce qui signifie que la colonne sera entièrement noircie, puisque les colonnes de la grille font 5 cases.
Regardons maintenant la deuxième ligne, où se trouve la séquence 3 1. Comme déjà dit, ceci signifie qu’il y a 3 cases à remplir, suivies de cases vides, puis 1 autre case. Comme on a au minimum 1 case vide, la ligne nous prend au minimum 3 + 1 + 1 = 5 cases. Comme la ligne comporte 5 cases, on peut la remplir :
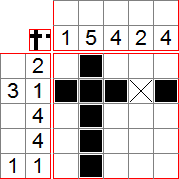
Nous allons maintenant placer des croix : si on regarde la première ligne, on remarque qu’il est impossible de remplir les deux dernières cases, puisque la deuxième est déjà remplie et qu’on doit remplir deux cases consécutives. On y met donc des croix. On remarque aussi que la première colonne est terminée, car il nous faut 1 case qu’on a déjà. On met donc des croix dans les 4 autres cases :
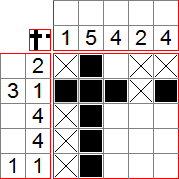
Ainsi, nous pouvons remplir les première, troisième et quatrième lignes, de même que la cinquième colonne, ce qui termine le tableau :
Nous avons obtenu un magnifique petit chien !
Méthodes de résolution
Dans ce paragraphe, nous allons présenter les principales méthodes de résolution. Nous les présenterons sur les lignes, mais elles sont évidemment valables aussi pour les colonnes. La plupart des grilles simples peuvent se résoudre en raisonnant « par colonnes » puis « par lignes » comme ci-dessus, et en répétant jusqu’à ce que la grille soit complète. Mais on ne peut pas toujours finir comme ça. Il faudra parfois raisonner par contradiction (« et si ? »), c’est-à-dire supposer une case remplie/vide, et en arriver à la conclusion que cette supposition rend le puzzle impossible. Dit ainsi, ça fait peur, mais vous verrez qu’il y a des techniques très simples de ce genre de raisonnement !
1) Chaînes
C’est la méthode la plus simple et qui permet souvent de remplir un bon nombre de cases. Nous l’expliquons par l’exemple. Prenons une ligne de longueur 10, avec comme chiffre-indice un 8.
On remarque qu’il y a seulement trois possibilités de remplir cette ligne, à savoir :
On voit donc que peu importe la solution de la ligne, certaines cases sont forcément pleines. Donc on peut les remplir de façon sûre :
Plus généralement, il suffit de considérer les deux situations extrêmes, c’est-à-dire, en commençant de la gauche, puis de la droite. Si on a des lignes avec plusieurs chiffres-indices, il faut considérer le cas extrême, à savoir qu’il n’y a toujours qu’une seule case vide entre les groupes de cases remplies, et considérer le tout comme une chaîne plus grande, contenant la case vide. Par exemple :
On a donc considéré la chaîne 4 + 1 + 3 = 8 comme une chaîne de 8 cases comme juste avant. On remarque qu’on peut donc cette fois remplir 3 cases de manière sûre :
ATTENTION ! Il aurait été faux de remplir la case 6, par exemple :
est une solution potentielle pour cette ligne, mais la case 6 est vide.
Pour vous faciliter la tâche, voici une façon de procéder à coup sûr avec cette méthode :
Compter la longueur de la chaîne, et regarder le décalage maximal possible :
- Ligne 1 : 3 + 1 + 3 + 1 + 3 = 11. Nous avons 15 cases à disposition, donc un reste de 15 – 11 = 4. Comme 4 est plus grand que 3, nous ne pouvons rien dire sur cette ligne.
- Ligne 2 : 3 + 1 + 3 + 1 + 4 = 12. Le reste est donc de 15 – 12 = 3. 4 est le seul chiffre-indice plus grand que 3, donc nous savons que la quatrième case du groupe de 4 est remplie (donc, en partant du bord droit, la quatrième case)
�
�
- Ligne 3 : 1 + 1 + 2 + 1 + 4 + 1 + 3 = 13. Le reste est donc de 15 – 13 = 2. 3 et 4 sont plus grands que 2, donc en partant de la droite, la troisième case du groupe de 3, ainsi que les troisième et quatrième cases du groupe de 4 sont remplies (donc, en partant du bord droit, la troisième et les septième et huitième cases)
�
2) Espaces simples
Considérons une ligne déjà partiellement remplie :
On constate que la case remplie à droite est forcément celle qui correspond au chiffre-indice 1. Ainsi, on peut mettre des croix à sa gauche et à sa droite. Le carré de gauche appartient forcément au groupe de 3. Ce groupe ne pourra jamais atteindre la première case, ni la septième, donc on peut y mettre des croix.
Voici un autre exemple d’utilisation :
La case déjà remplie appartient forcément au groupe de 2, car on ne peut pas mettre le groupe de 2 dans les deux premières cases (sinon ce serait un groupe de 3). On peut donc mettre une croix en première case. Puis on peut appliquer la méthode 1) sur la ligne des 9 cases restantes, en trouvant un reste de 1 :
3) Le forçage
Voici une situation :
Le groupe le plus court étant de longueur 2, il n’est pas possible de remplir la case 6, sinon elle serait isolée. On y met donc une croix. Il en résulte que forcément, le groupe de 3 est avant les croix, et celui de 2 est après. Par la méthode 1) on peut remplir partiellement ces groupes.
4) Le collage
Voici deux situations :
- Première ligne : Le groupe de 5 va forcément continuer jusqu’à la case 5 au moins (on ne peut pas mettre de croix en cases 4 ou 5, sinon il est impossible de placer un groupe de 5). On peut ensuite mettre quelques croix par la méthode 2).
- Deuxième ligne : La première case est seule, donc on met une croix en case 2. Le groupe de 3 va forcément continuer jusqu’à la case 6 au moins. On ajoute des croix par la méthode 2).
�
5) Connecter et séparer
Voici une situation :
Supposons que l’on remplisse la première case. Ce n’est pas possible, car on aurait un groupe de 7. Donc forcément, on doit remplir la case 5 et former ainsi un groupe de 5. De même, supposons qu’on noircisse la case 12. Ce n’est pas possible, car on aurait un groupe de 3, et on doit avoir des groupes de 2. On met donc une croix. On complète ensuite avec les règles précédentes.
En règle générale, deux cases remplies séparées par un espace sont :
- connectées si mettre une croix ferait des groupes trop courts ;
- séparées par une croix si remplir la case ferait un groupe trop long.
�
Exemple (difficile) appliquant les techniques précédentes
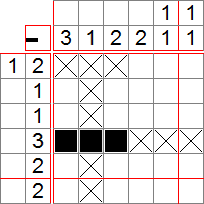
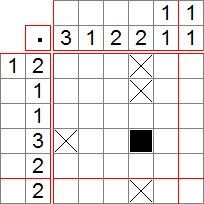
On voit qu’aucune méthode simple ne nous permet de placer des croix ou remplir des cases. Intéressons-nous à la ligne 4. Supposons que la case 4 de cette ligne soit une croix. Ainsi, nous pouvons remplir la ligne. On applique ensuite la méthode 2) pour mettre des croix :
Ceci nous entraîne à une contradiction, car on ne peut plus remplir la première ligne (on a besoin de 4 cases et on n’en a que 3). Ainsi, la case 4 de la ligne 4 est remplie ! On applique 2) pour mettre des croix.
On peut donc utiliser 3) sur la première colonne et la première ligne, puis mettre des croix pour remplir et finir les lignes/colonnes concernées.
On continue simplement en appliquant les méthodes :
Cet exemple montre qu’un picross n’a pas forcément une unique solution (cependant, pour Pokémon Picross, les développeurs se sont arrangés pour éviter les solutions multiples). Voici les deux solutions possibles :
Conseils
- Ne remplissez une case que si vous êtes sûr. Sinon, vous risquez de mettre une faute dans votre picross, et les fautes sont souvent difficiles à corriger, car une faute en induit d’autres. Pour pallier à ce problème, n’hésitez pas à utiliser un pouvoir Autocorrecteur.
- Donnez toujours une priorité aux cases sur les bords, comme ça vous pouvez utiliser la méthode 2. Si vous utilisez une bombe et que vous pouvez choisir où l’utiliser, choisissez à une ou deux cases du bord, le picross n’en sera que plus facile !
- N’hésitez pas à utiliser un pouvoir Force Bleue, surtout au début, pour vous faire prendre le coup !
�
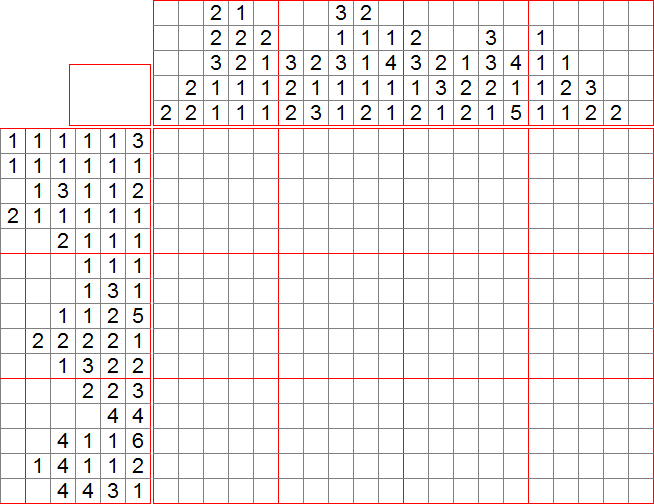
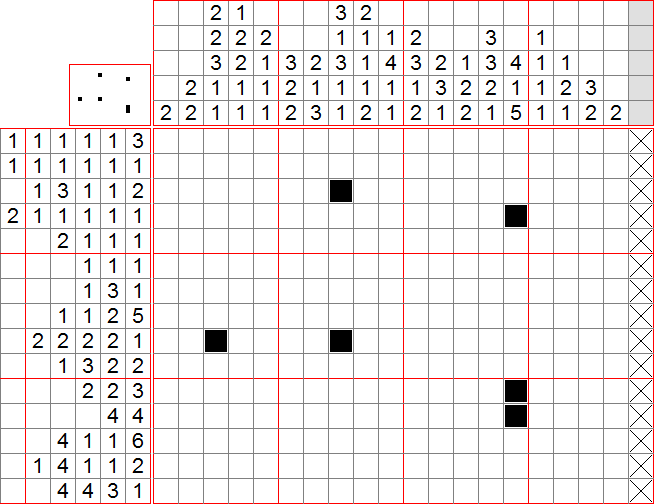
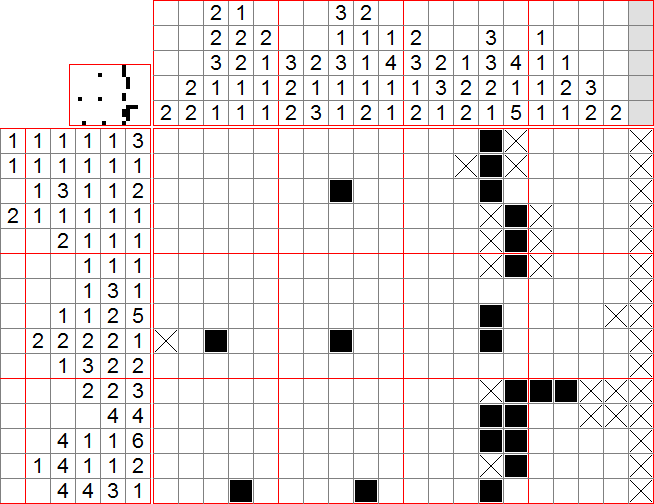
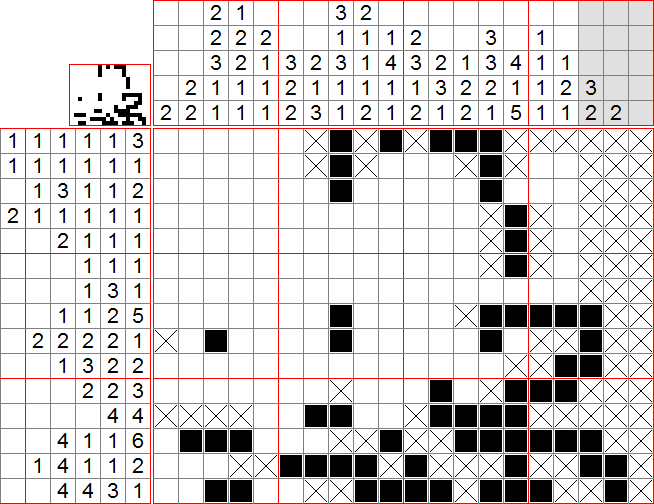
Exemple tiré du jeu : Niveau 04-08
Voici le niveau 04-08 du jeu. Nous allons le résoudre ensemble. Les images sont sous spoiler pour gagner de la place et inciter à la réflexion personnelle.
On commence bien sûr par mettre des croix sur toute la dernière colonne. Puis on applique la méthode 1 sur chaque colonne. On peut ainsi mettre des cases dans les colonnes 3, 8 et 14.
Ensuite on regarde les lignes : la case remplie de la ligne 4 est forcément isolée, la première case de la ligne 9 ne peut pas être remplie (méthode 2), de même pour la dernière case de la ligne 17. On peut placer deux cases sur la ligne 18 par la méthode 1.
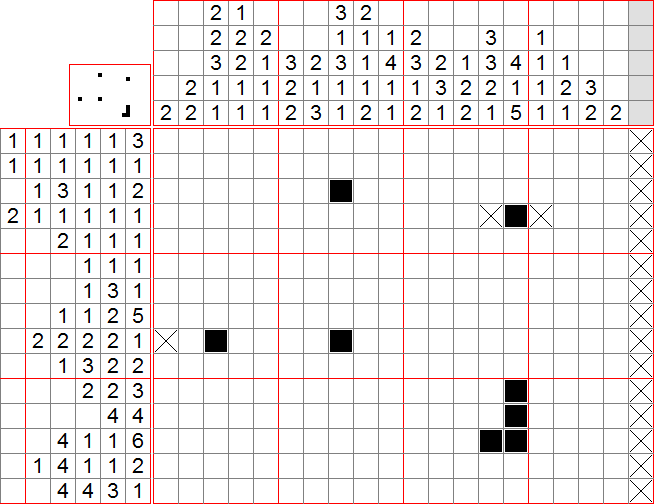
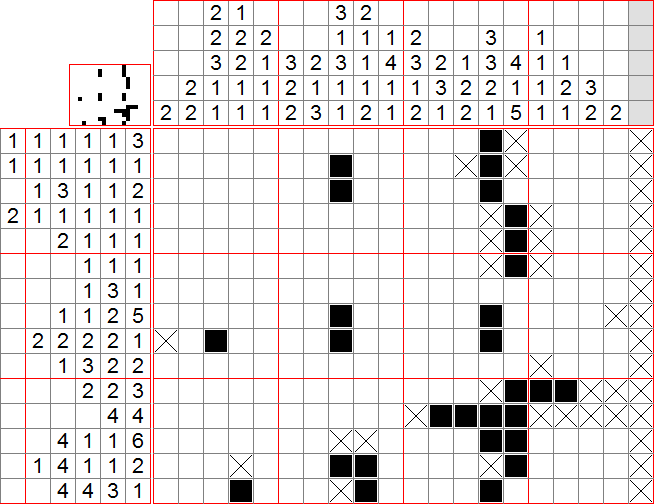
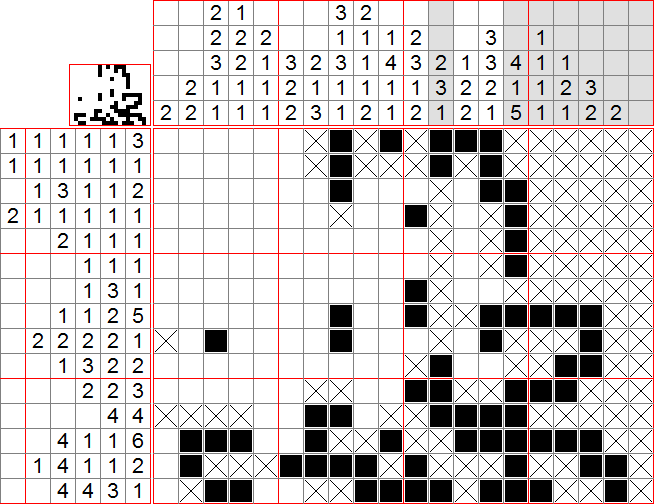
On peut ensuite appliquer la méthode 2 à la colonne 14 et mettre une croix dans l’avant-dernière case (autrement, on aurait un groupe de 2, ce qui est impossible). Par la méthode 3, on peut aussi remplir les 3 premières cases en haut de cette colonne. On peut ensuite isoler la case tout juste ajoutée en ligne 2 (car ne contient que des 1).
Ensuite, on peut utiliser les méthodes 3, 4 puis 1 sur la colonne 15, et donc mettre une croix tout en haut, remplir les cases 5 et 6, et la 14. On isole ensuite les cases ajoutées en lignes 5 et 6. Ceci nous permet d’appliquer la méthode 3 à la colonne 14, et ainsi remplir les cases 8, 9, 12 et 15, et mettre une croix en case 16.
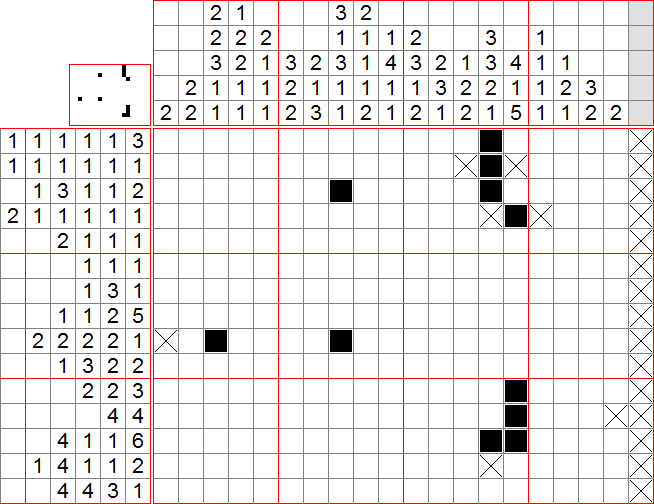
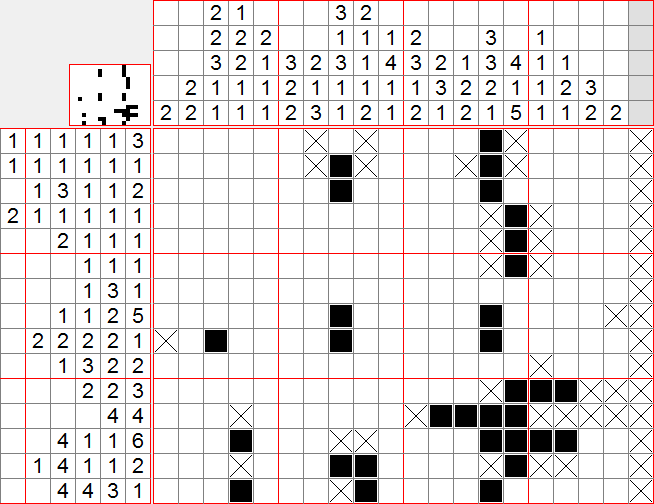
Maintenant, reprenons les lignes : on peut appliquer la méthode 2 à la ligne 8, la 3 à la ligne 11, la 2 à la ligne 12. Pour la ligne 15, on remarque que la case noircie fait forcément partie du groupe de 3 (compter depuis la gauche et depuis la droite) donc on peut appliquer la méthode 1 aux indices (4 4 3) sur les 16 premières cases de la ligne (reste de 3)
On peut ensuite remplir les bords inférieurs des colonnes 4 et 9, et isoler la case ajoutée en colonne 16, ce qui nous permet de trouver un groupe de 4 de la ligne 12. On compte ensuite la ligne 14 : le cas extrême est : la première case isolée avant la première croix, puis la chaîne (1 2) tout au bout. Il reste donc la chaîne (4 1) à placer entre les cases 5 et 13. En appliquant 1, on peut remplir la case 8. Ceci nous permet d’isoler cette case dans la colonne 8, et par suite d’y appliquer 1 à nouveau pour remplir les cases 2 et 8 de la colonne 8.
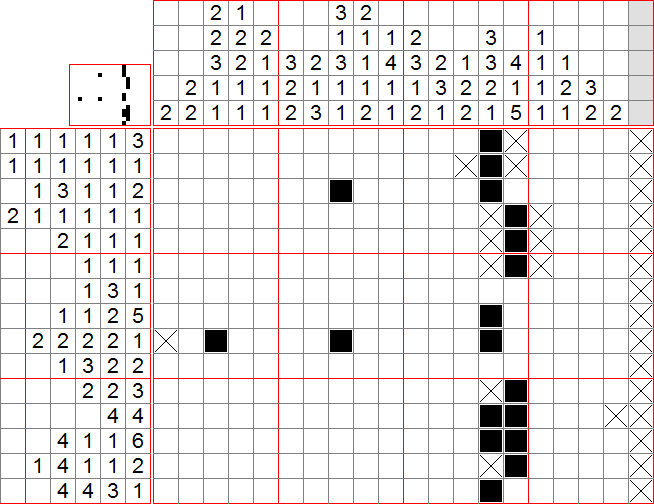
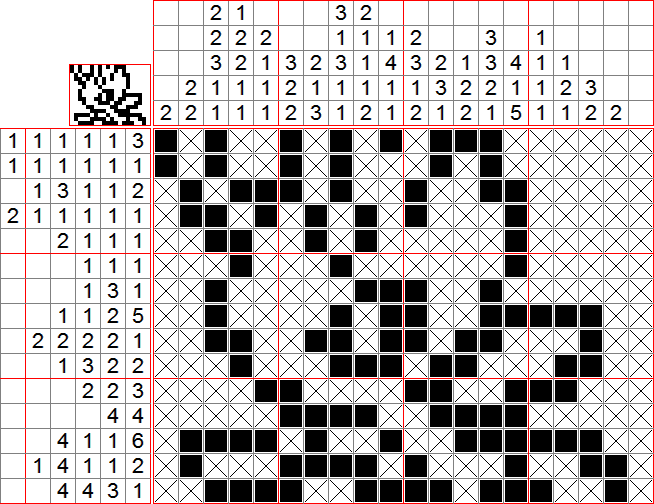
On peut donc isoler la case ajoutée en ligne 2, et placer des croix tout en haut des colonnes 7 et 9. Intéressons-nous à la ligne 13 : le groupe de 4 se trouve forcément dans les 7 premières cases, donc on remplit la case 4 (qu’on isole directement verticalement). En comptant sur la ligne, on constate que dans les cases 10 à 19, nous devons placer au moins la chaîne (1 6), donc nous pouvons remplir les cases 16 et 17 (et les isoler verticalement)
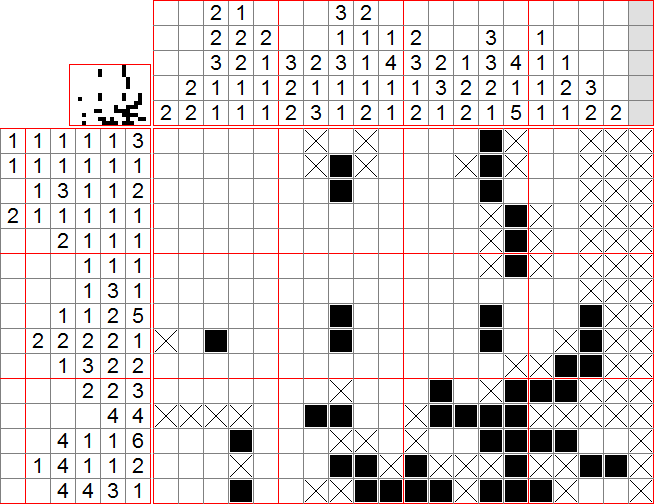
On peut donc (instructions sous spoiler car longues) :
�
Nous présentons maintenant un petit raisonnement facultatif, mais qui pourrait être nécessaire ailleurs : En ligne 15, il faut forcément remplir soit la case 18, soit la case 19. Cependant, si on remplit la case 18, alors on devrait remplir la case 19 de la ligne 13 et mettre une croix dans la case 18 de cette ligne. Donc nous n’aurions pas le groupe de 6. Donc, pour préserver la continuité du groupe de 6, il faut remplir la case 19 de la ligne 15. Par suite (instructions sous spoiler) :
�
Ensuite (instructions sous spoiler) :
�
C’est bientôt fini ! Les dernières instructions sont toutes élémentaires et nous les mettons en spoiler en raison de leur nombre (et simplicité).
�
Et voilà ! Un magnifique Celebi !
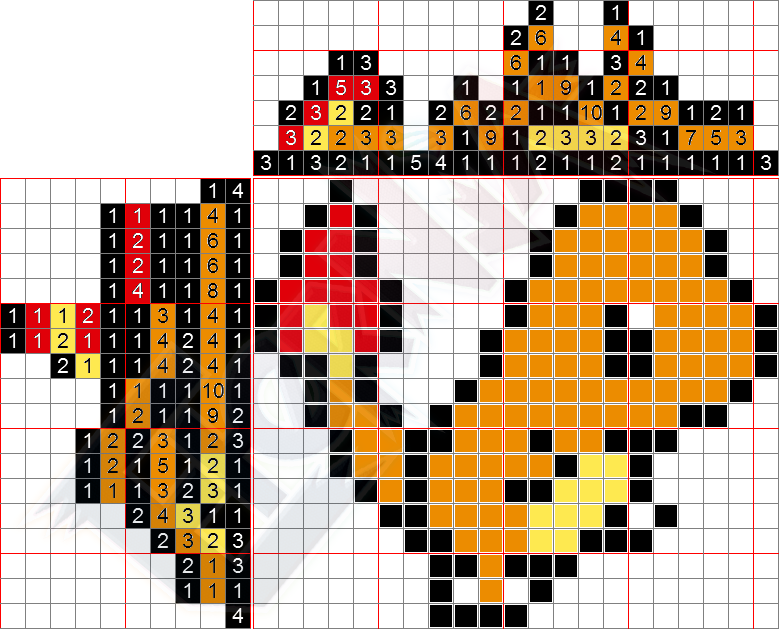
Aller plus loin : Les picross colorés !
Ils ne sont pas présents dans le jeu directement, mais quand vous résolvez une grille, elle se colorie. Nous vous présentons juste le concept de picross coloré : C’est comme le picross habituel (binaire) mais avec plusieurs couleurs. Voici une ligne d’un tel picross en guise d’exemple.
On remarque donc qu’ici, on ne sait jamais où se trouvent les cases avec des croix, car il n’y en a pas forcément entre deux couleurs différentes !
Si vous voulez vous amuser avec un picross coloré, en voici un (avec sa solution) :
Cet article a été mis à jour pour la dernière fois le 01/02/2016 à 11:00.
Vous avez remarqué une erreur, une quelconque faute d'orthographe ou autre sur cette page ? N'hésitez pas à nous en faire part ! :)